Boolean Complex Geometry

by Clark Cheng

Icon

Boolean SOP in Houdini is great but sometimes it doesn't work with stubborn geometry, even if its already closed. I was looking online for other options and decided to learn how does a "Boolean" operation work. I came across this research paper on how they calculate complex mesh geometry fast.

They're 3 types of boolean operations:

  1. Boolean Difference or Subtraction
  2. Boolean Union
  3. Boolean Intersect

The steps that are included for the fundamentals of a boolean is:

We will name the geometry A and B for simplicity sake.

  1. Split geometry A with B and vice versa
  2. Choose which parts to keep
  3. Fuse and Retriangulate

In this example, I will show a boolean difference.


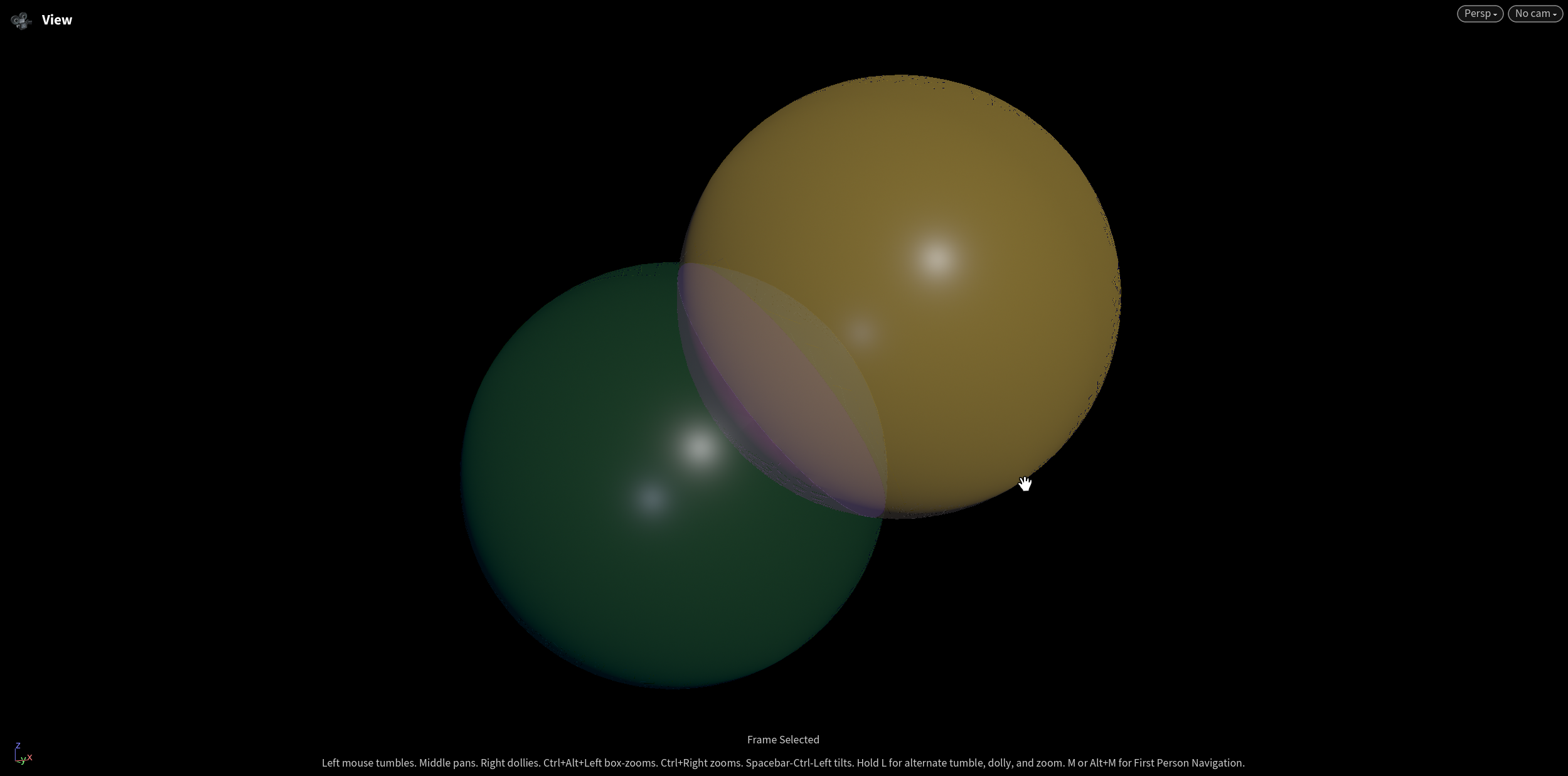
Image 8

2 spheres as text geometry.


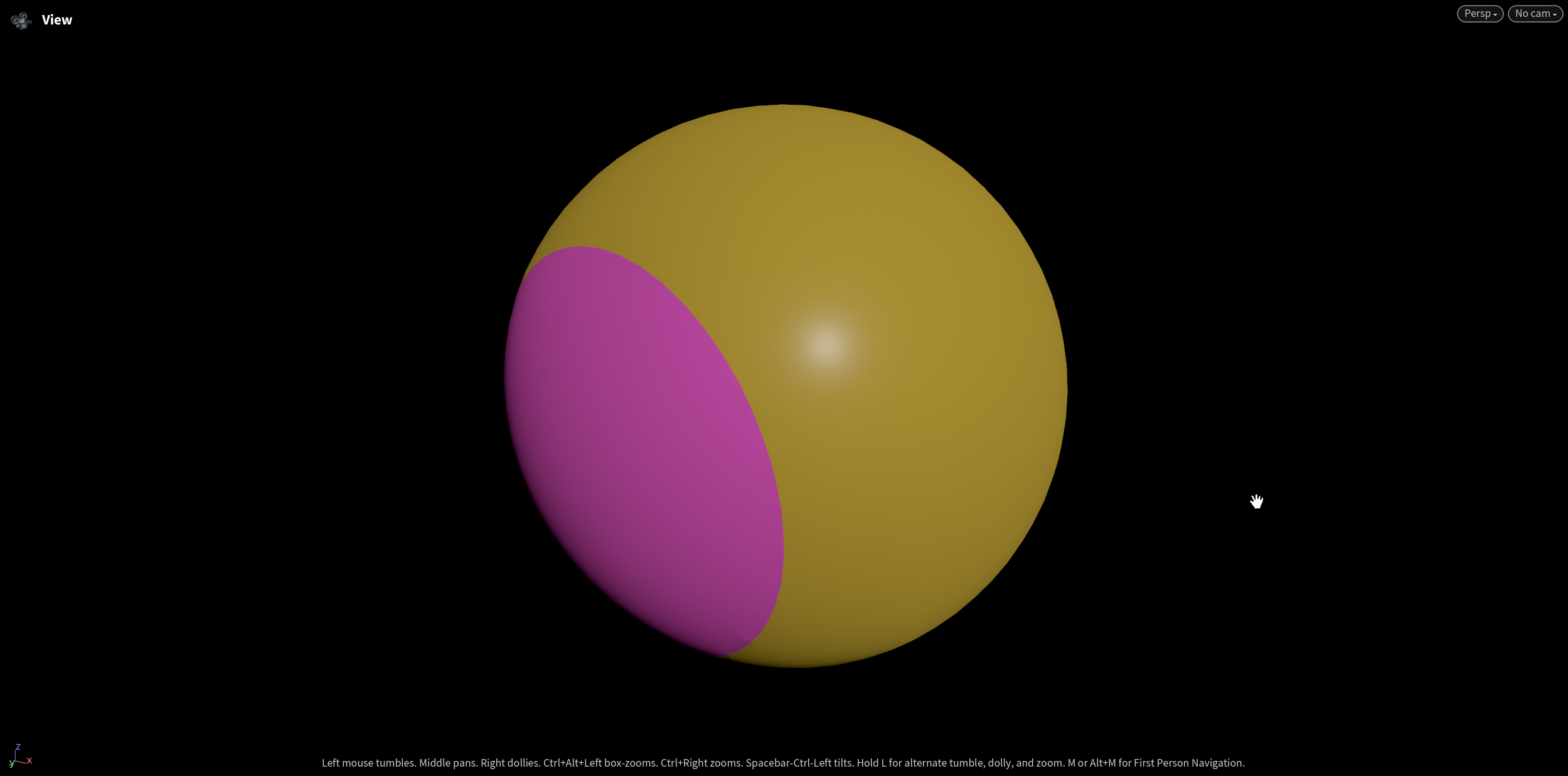
Image 4

Solid view of the 2 sides (pink and yellow)


Image 6

Solid view of the 2 sides (green and teal)


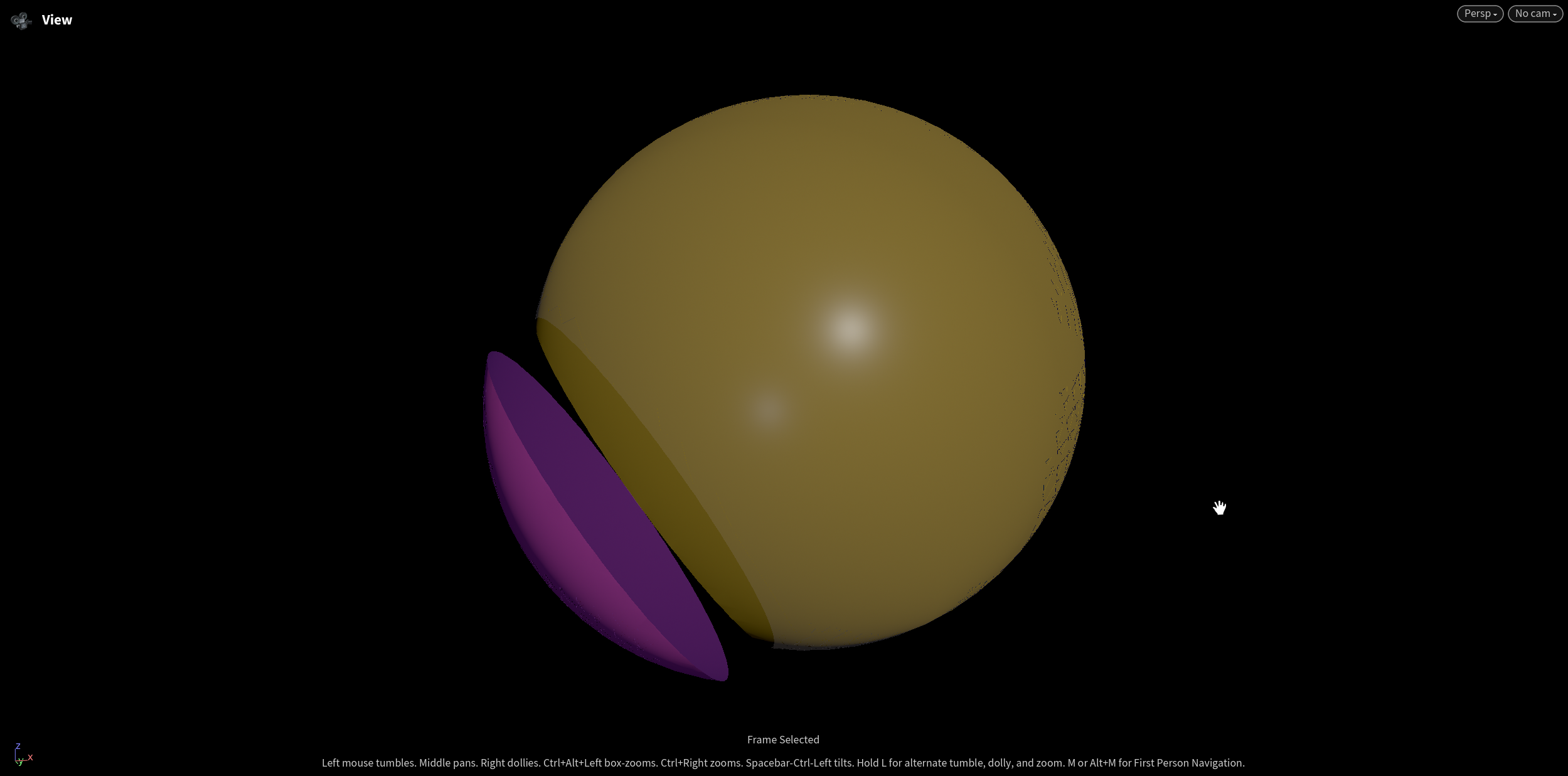
Image 9

Mesh A and the intersection of the Mesh A and B.


Image 7

Mesh B and the intersection of the Mesh A and B.


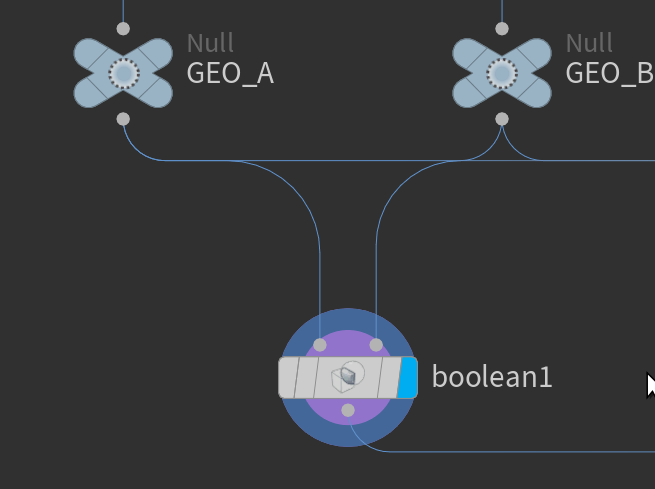
Image 1

Connect the geometries like a normal with the Boolean SOP.


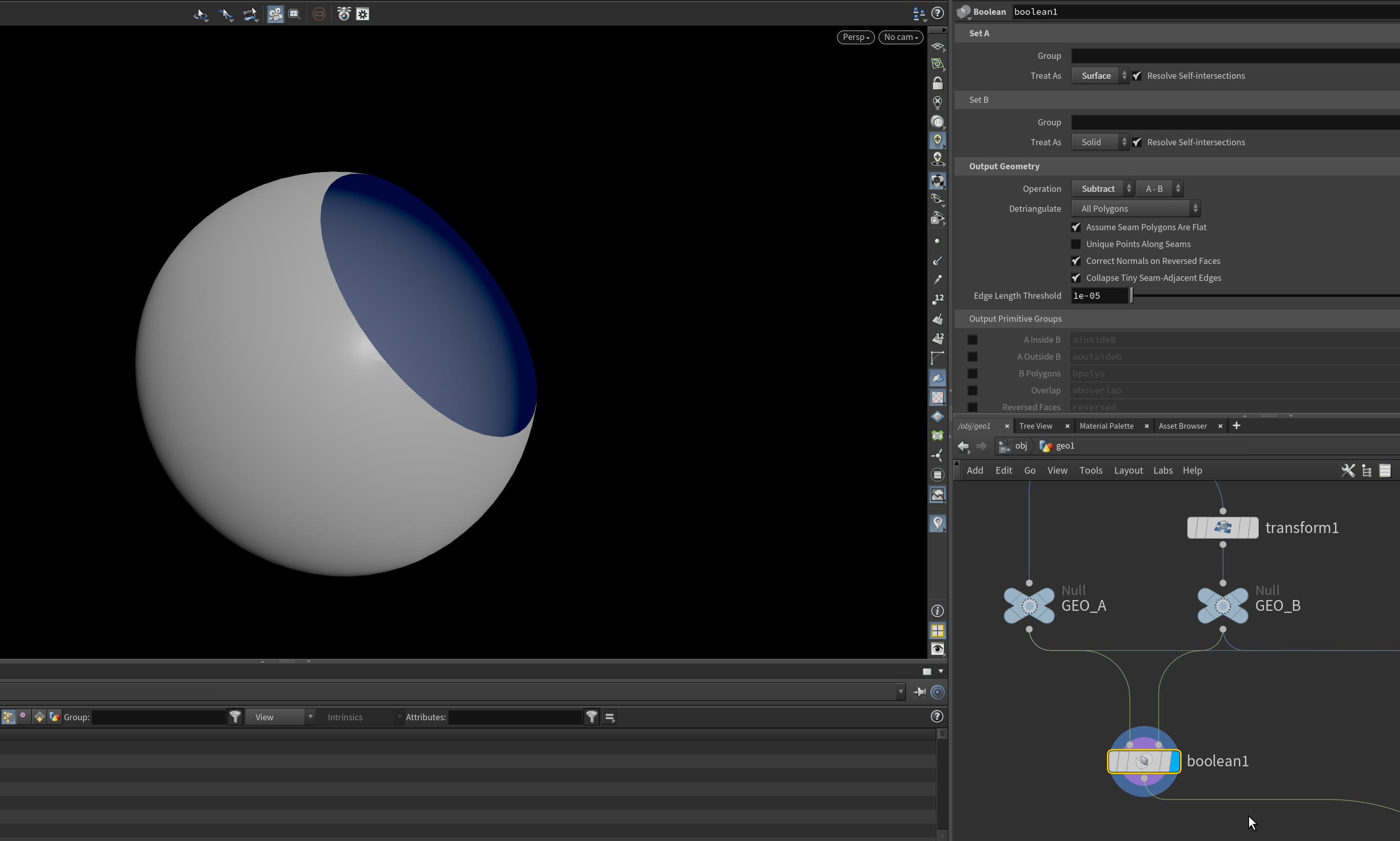
Image 10

Change Solid A to "Surface".


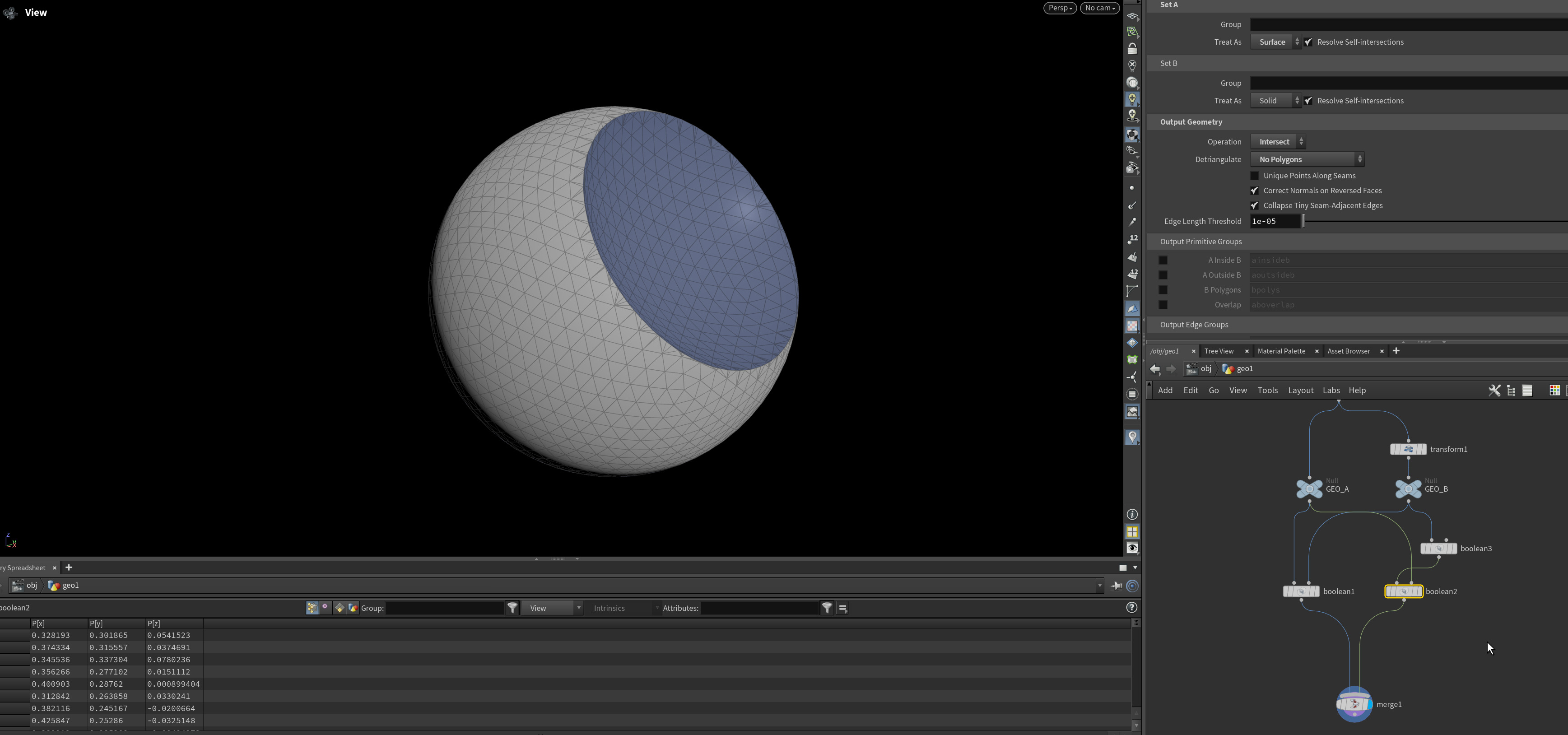
Image 12

When we merge the two resulting booleans, we get both sides. We can see one face is reversed.


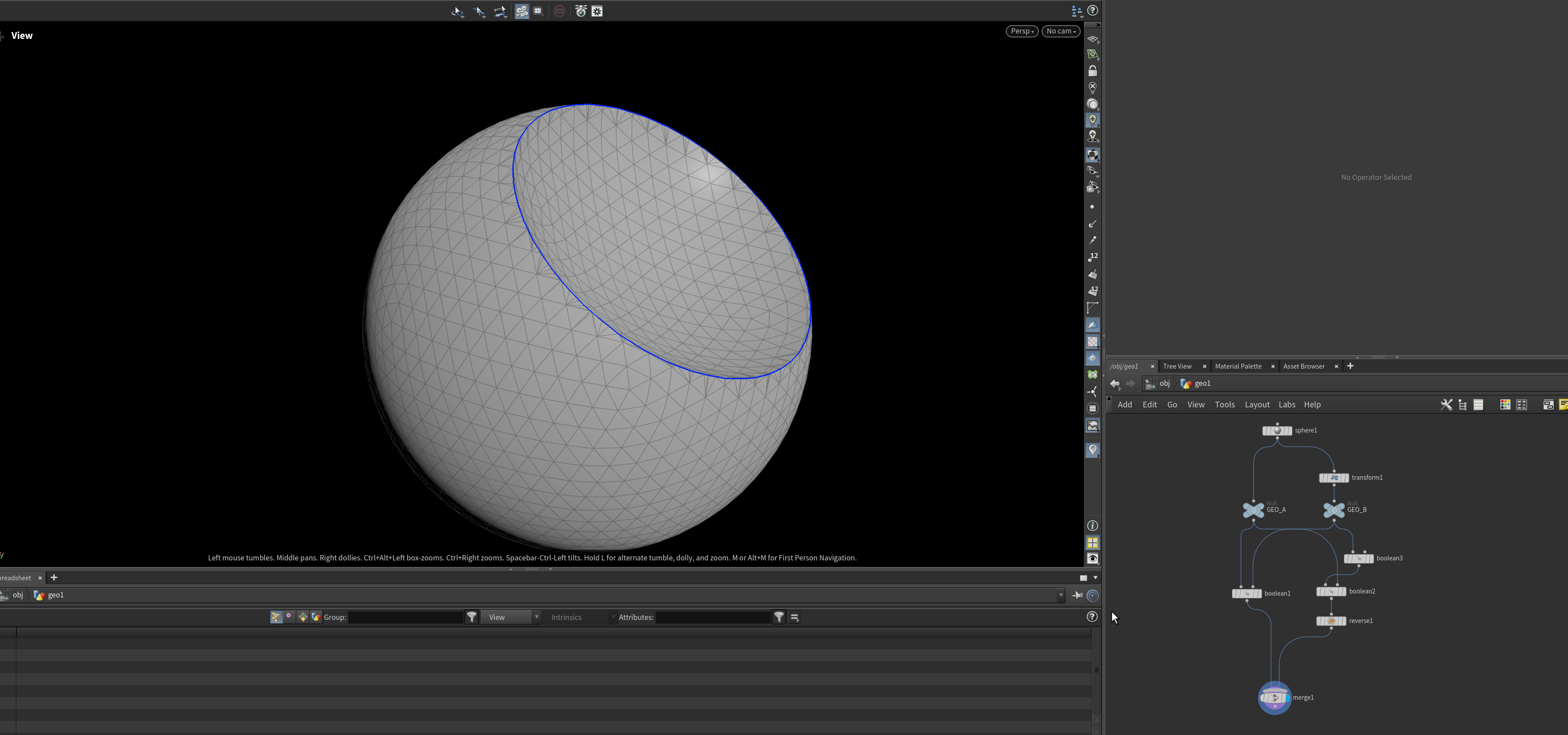
Overview

The two sides of the mesh are aligned, but not joined, highlighted in blue.


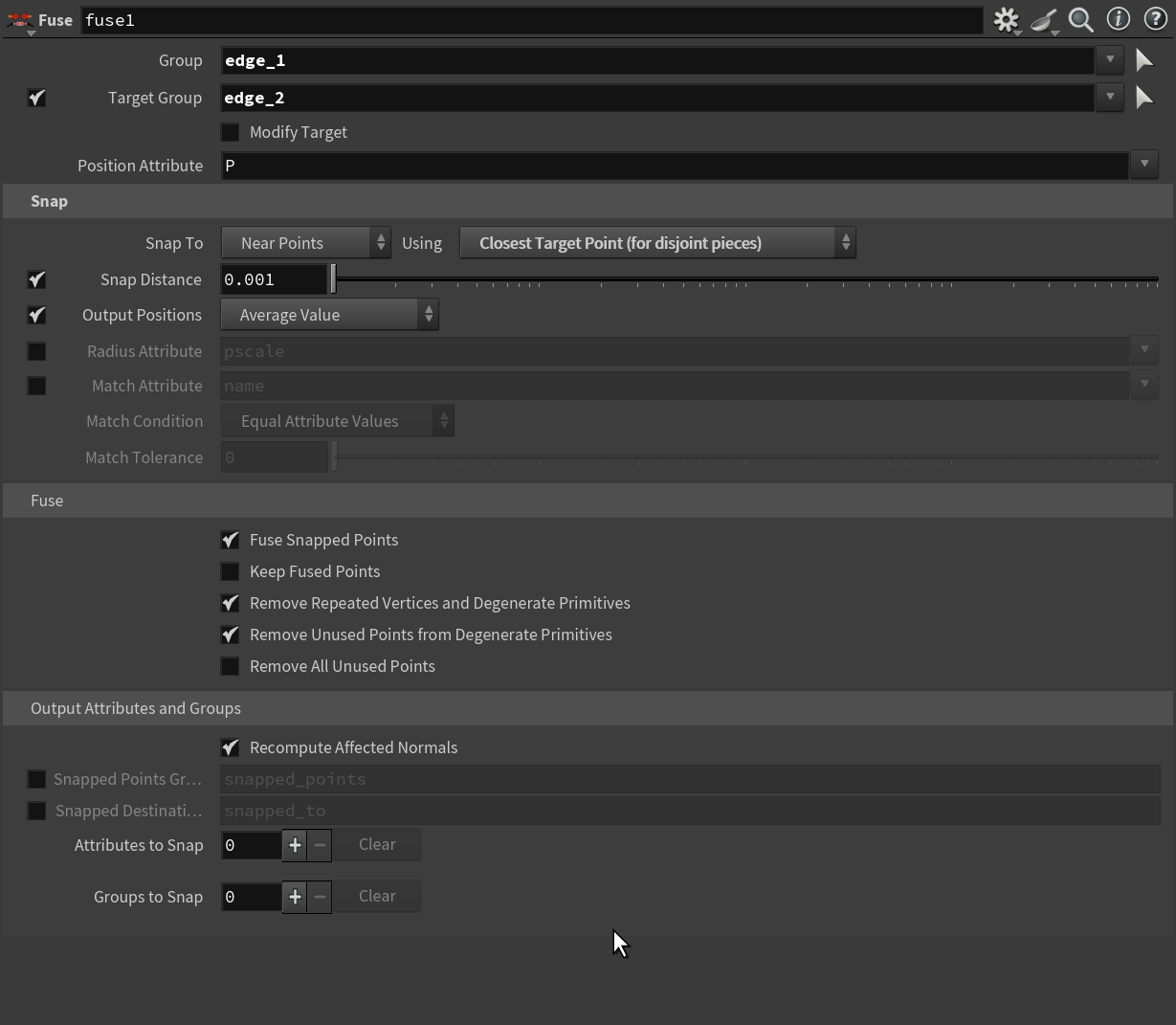
Image 2

Using Fuse SOP, we can join them all together.


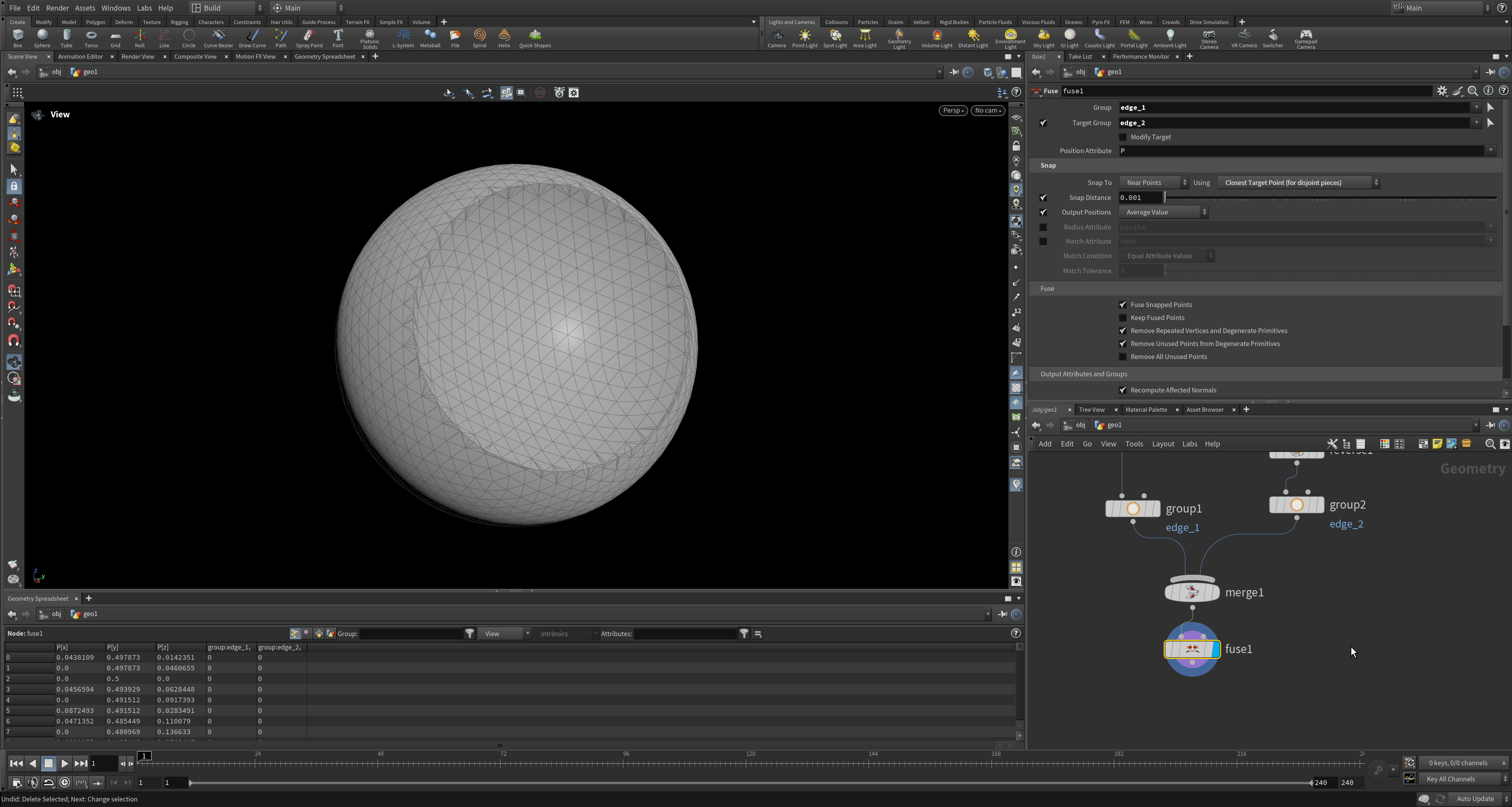
Image 5

Resulting Fuse SOP results. Fully closed mesh, but with triangle fanning.


This setup allows for large amounts of geometry to be boolean'd all at once. Here are some other examples of more complex geometry

  1. Sphere-Sphere subtraction
  2. Rubber toy subtraction
  3. Pig geometry subtraction

Complex Boolean 2
Complex Boolean 2
Complex Boolean 2


Understanding how boolean operations work under the hood not only helps troubleshoot issues in Houdini but also opens the door to more custom and optimized workflows. While Houdini's Boolean SOP is powerful, knowing the fundamental steps—splitting, selecting, and fusing geometry—can give you the flexibility to manually intervene when things go wrong or build your own tailored tools. In the next part, I'll walk through a practical example of a boolean difference operation and break down how each step applies in practice.