Triple Product Concept

by Clark Cheng

Posted on January 4, 2025 at 9:00 PM

So what exactly is the triple product anyways?

The triple product is a way to combine three vectors to find useful geometric or physical properties. The scalar triple product measures the volume of a 3D shape made by the vectors, telling you if they are aligned or coplanar. The vector triple product gives a new vector that stays in the same plane as two of the original vectors, helping with directions and alignments.

Triple Product in Mathematics

The triple product in mathematics refers to the scalar triple product or the vector triple product, depending on the context. Here's a simple breakdown:

Scalar Triple Product

Formula: \( \mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) \)
Purpose: Measures the volume of the parallelepiped formed by the three vectors \( \mathbf{a}, \mathbf{b}, \mathbf{c} \).
Application: Useful for determining whether vectors are coplanar (result is zero) or for calculating volumes in 3D geometry.

Vector Triple Product

Formula: \( \mathbf{a} \times (\mathbf{b} \times \mathbf{c}) \)
Purpose: Results in a vector that lies in the plane of \( \mathbf{b} \) and \( \mathbf{c} \).
Application: Common in simulations and solving geometry problems.

Both tools involve vector math heavily, so understanding the triple product gives you a strong foundation for procedural and parametric systems.

Triple Product and Frenet Frame in Grasshopper

This Grasshopper script builds a Frenet-like frame using a sequence of vector operations. The result visually resembles a tangent-normal-binormal system, and the key construction involves a vector triple product.

Step-by-Step Breakdown

Input Curve: The Curve component provides the geometry to sample from.
Divide Curve: The Divide Curve component outputs:
- Points – sample locations along the curve.
- Tangents – direction vectors at each point (denoted \( \mathbf{T} \)).
- Parameter – Gives the parameter values of the points on the curve., from 0 to 1. We will not use it here, but useful to know.
Reference Vector: The Unit Z component gives the vector \( \mathbf{Z} = (0, 0, 1) \), acting as a stable up-axis.
First Cross Product: Computes \( \mathbf{N}' = \mathbf{T} \times \mathbf{Z} \), a vector orthogonal to the tangent and global Z. This approximates a local binormal.
Second Cross Product (Triple Product): Computes

\( \mathbf{B} = \mathbf{T} \times (\mathbf{T} \times \mathbf{Z}) \)

This is the vector triple product. The result lies in the plane defined by \( \mathbf{T} \) and \( \mathbf{Z} \), and is orthogonal to \( \mathbf{T} \), acting as a "normal".
Scaling Vectors: A slider controls the visual length of each vector by multiplying them before display.
Vector Display: Three Vector Display components show the Tangent, Normal (from triple product), and Binormal (first cross product) at each point along the curve.

This setup uses the identity \( \mathbf{a} \times (\mathbf{b} \times \mathbf{c}) \) to construct a stable frame along a curve, which is visually and practically similar to a Frenet frame but avoids issues with noisy curvature.

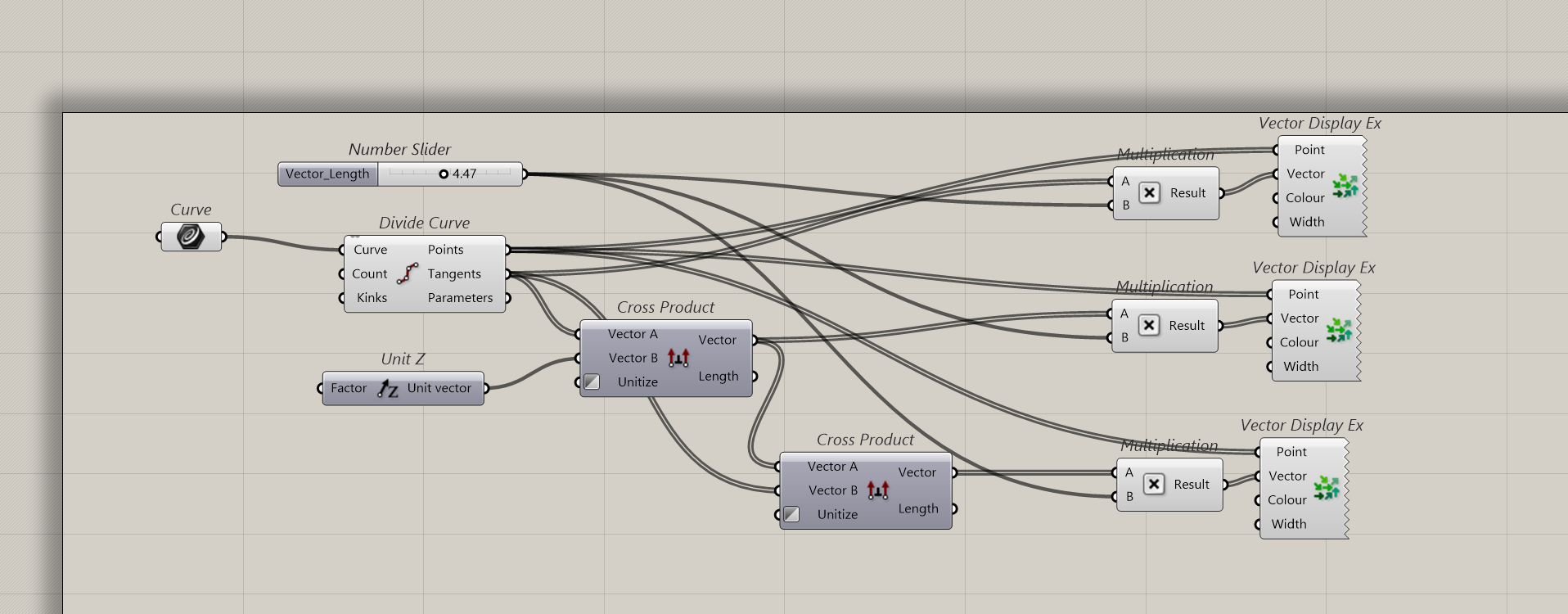
This Grasshopper script constructs a local coordinate frame along a curve using the vector triple product. It starts by dividing the curve into evenly spaced points and extracting tangent vectors. A cross product between each tangent and the global Z vector produces a binormal. Then, another cross product between the tangent and that binormal yields a normal vector, effectively computing \( \mathbf{T} \times (\mathbf{T} \times \mathbf{Z}) \). All three vectors—tangent, binormal, and normal—are scaled and displayed at each point, forming an orthogonal frame suitable for geometric analysis or orientation tasks.

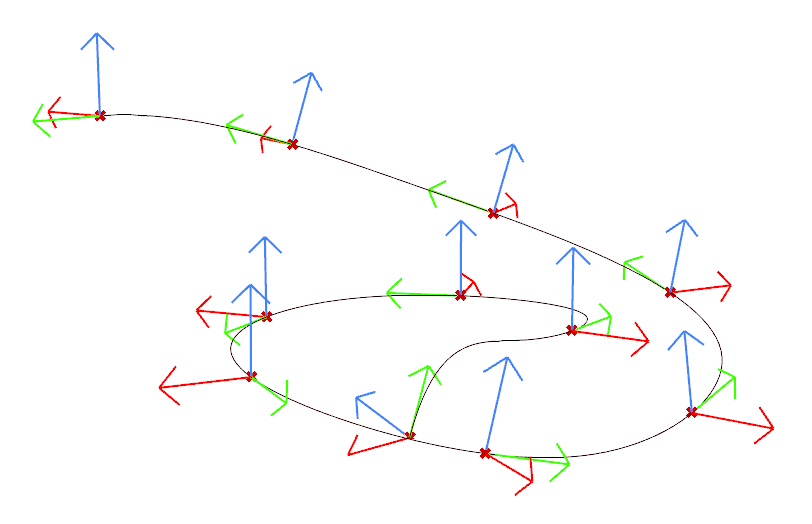
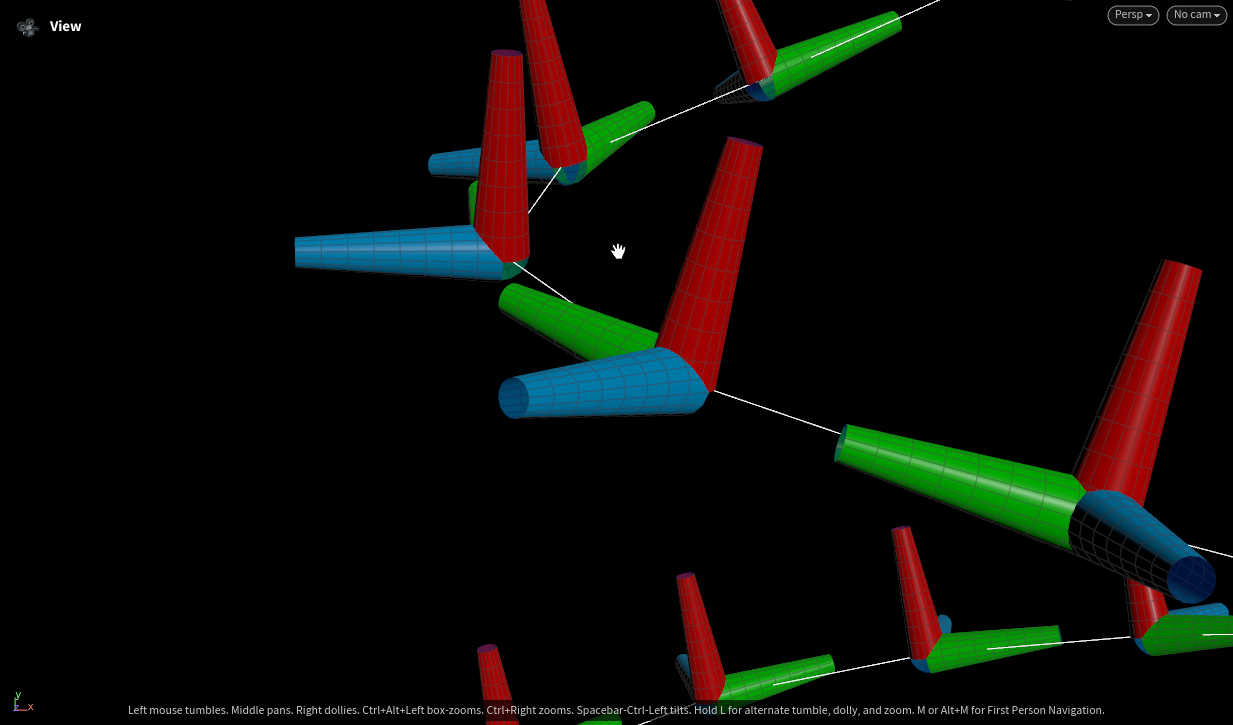
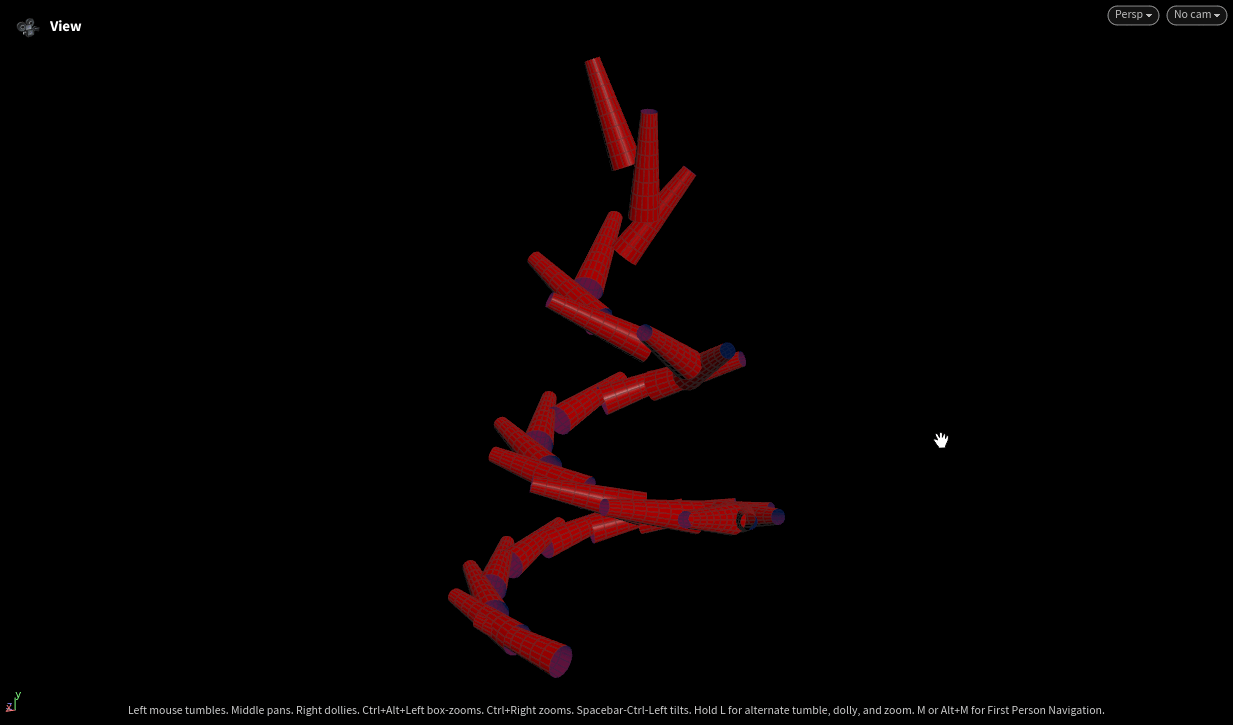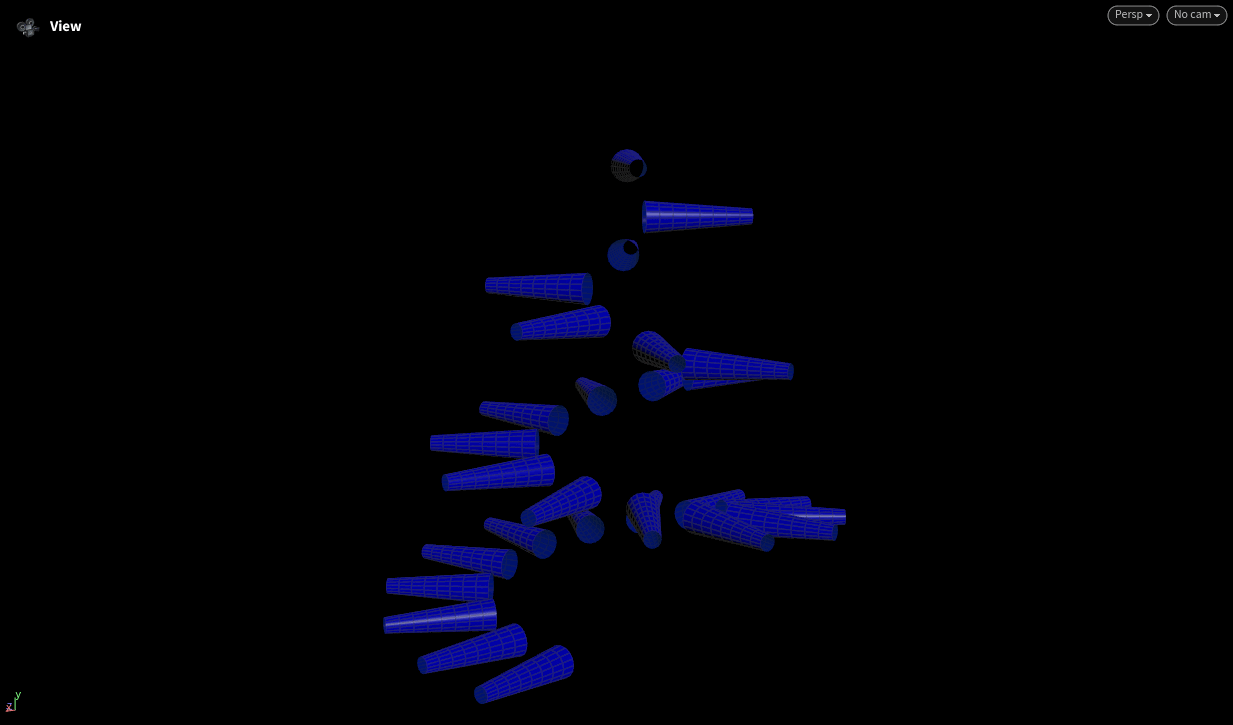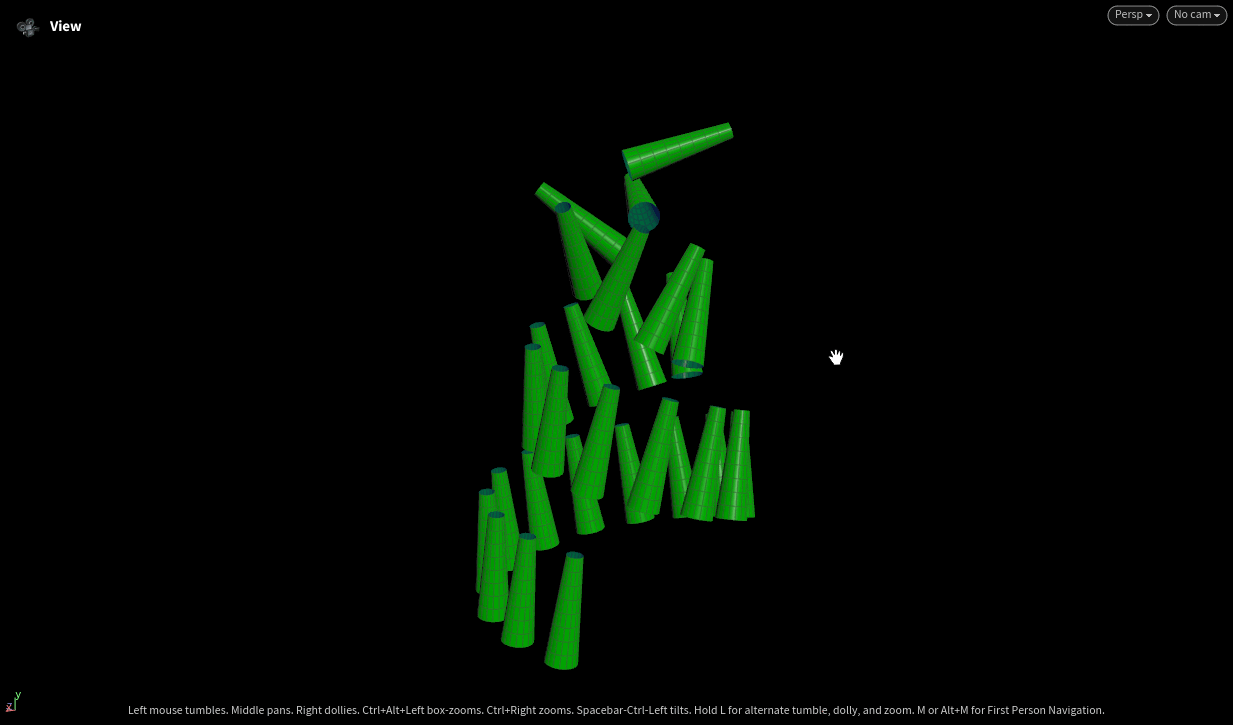
This Rhino viewport shows a spatial curve with orthogonal vectors—tangent (red), normal (green), and binormal (blue)—visualized at evenly spaced points along the curve. The vector directions form a local frame at each point, generated using a triple product construction in Grasshopper. This setup illustrates a stable orientation system for the curve, useful for geometry manipulation, animation, or procedural design.

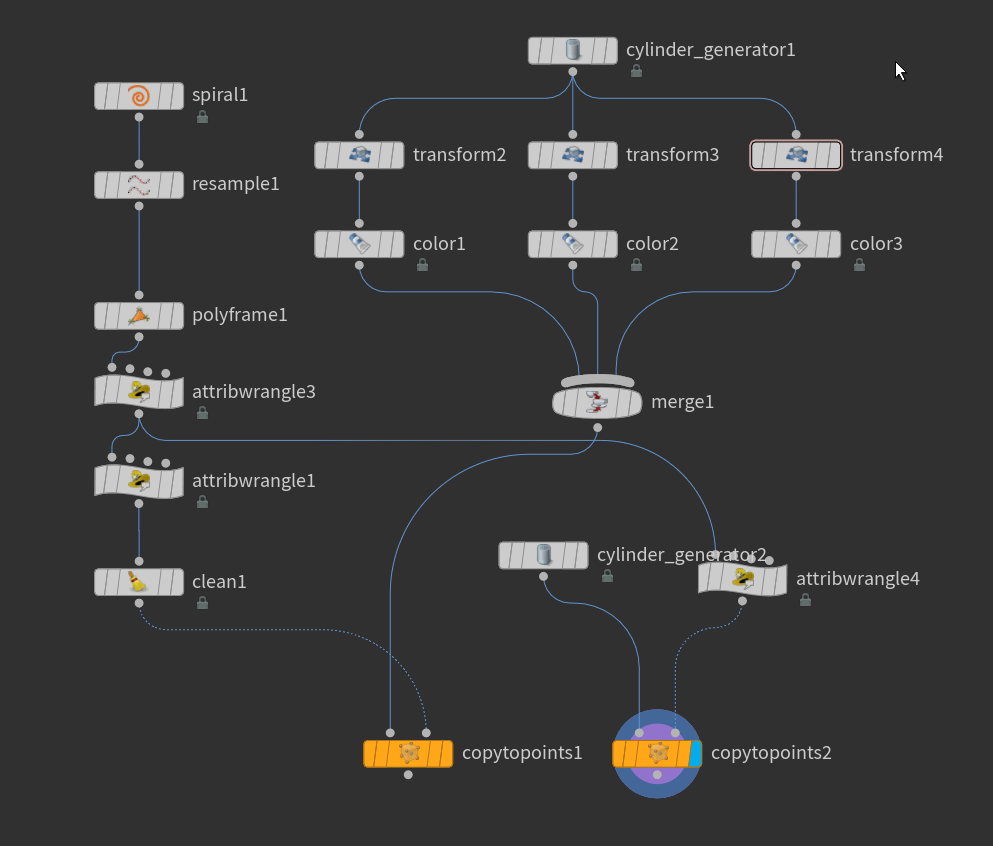
This Houdini script generates a spiral curve, computes normals using the PolyFrame SOP, and then applies a VEX wrangle to construct a vector triple product for orientation. Axis geometry is used to visualize the tangent, normal, and binormal vectors. Finally, geometry is copied to the points using the custom frame, aligning each instance with the local orientation.

This is the VEX script I made in order to demonstrate the triple product. This version creates a @orient, which CopytoPoints uses to align the geometry.


          //define y axis
          vector y = {0,1,0};


          //cross product 1
          vector rel_y=cross(@N,y);

          //reverse vector
          v@rel_y=rel_y*-1;

          //create frame, which turns into @orient
          matrix3 m = maketransform(v@rel_y,@N);
          p@orient = quaternion(m);

          //@N=v@rel_y;

This one shows each different axis and how you can switch between them as a method of alignment.


          //define y axis
          vector y = {0,1,0};

          //cross product 1
          vector rel_y=cross(@N,y);

          //reverse vector
          v@rel_y=rel_y*-1;

          //cross product 2
          v@rel_z = cross(@N,v@rel_y);

          //float
          float type = chi("type");

          //color
          @Cd={1,0,0};

          //goes to relative z
          if (type==1) {
          @N=v@rel_z;
          @Cd={0,1,0};
          }

          //goes to relative y
          else if (type==2) {

          @N=v@rel_y;
          @Cd={0,0,1};
          }